数据结构篇-2021春招准备

1、Hash原理

Hash算法较多的应用在数据存储和查找领域，最经典的就是Hash表，它的查询效率非常高，如果哈希算法设计的好，那么Hash表的数据查询时间复杂度可以接近于O(1)

Hash算法使用示例

提供一组数据1，5，7，6，3，4，8，对这组数据进行存储，然后随便给定一个数n，请你判断n是否存在于刚才的数据集中？

• 顺序查找法：这种方式就是通过循环来完成，比较原始，效率也不高
• 二分查找法：排序之后折半查找，相对于顺序查找法会提高一些效率，但是效率也并不是特别好
• 直接寻址法：直接把数据和数组的下标绑定到一起，查找的时候，直接array[n]就取出了数据
  • 优点： 速度快，一次查找得到结果
  • 缺点：
    • 浪费空间（数据：1，3，7，12306）
    • 单个索引上存储内容有限（数据：1，1，2，12，12，1，1）

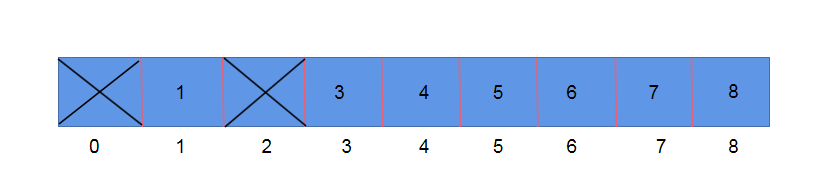
• 除留取余法: 根据求模余数确定存储位置的下标

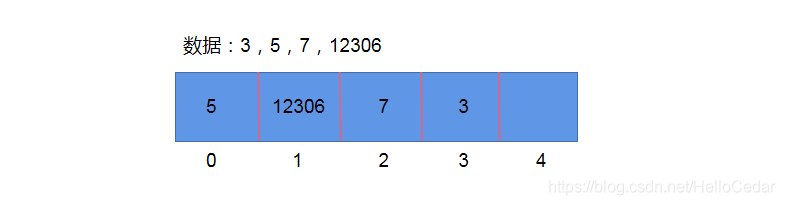
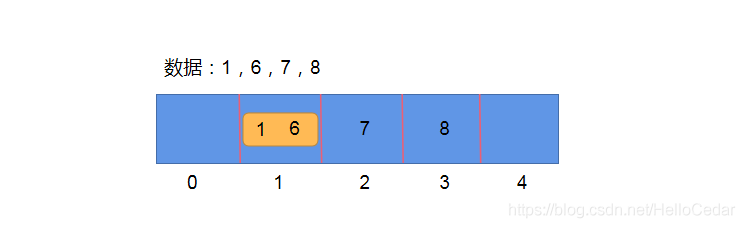
• 开放寻址法: 如果数据是 1，6，7，8 采用除留取余法则会造成hash冲突，此时可以采用开放寻址法，比如：1放进去了，6再来的时候，向前或者向后找空闲位置存放
  • 缺点： 如果数组长度定义好了，比如10，由于数组长度不能扩展，来了11个数据，不管Hash冲突不冲突，肯定存不下这么多数据

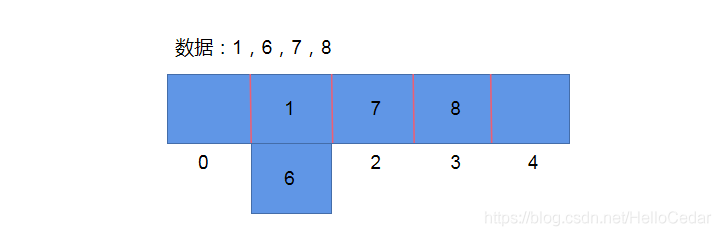
• 拉链法: 数据长度定义好了，怎么存储更多内容呢，算好Hash值，在数组元素存储位置放了一个链表

Hash算法应用

• 分布式集群架构Redis
  • 以分布式内存数据库Redis为例，集群中有redis1，redis2，redis3三台Redis服务器，那么，在进行数据存储时，<key1,value1> 数据存储，针对key进行hash处理 hash(key)%3=index，使用余数index锁定存储的具体服务器节点
• Hadoop
• ElasticSearch
• Mysql分库分表
• Nginx负载均衡

2、一致性Hash

原因: hash一般是将一个大数字分散到不同的桶里面，如果两个桶则%2。若扩容新桶所有的数字都需要%3，所有的数字分布都变了，即hash表每次扩容或收缩都会导致所有条目重新计算。

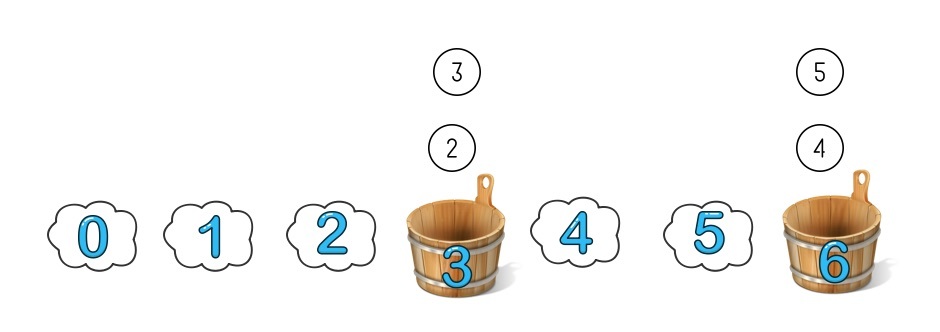
方案: 一致性hash中假想有很多桶，比如 7 个，但一开始真实还是只有两个桶，编号是 3 和 6。哈希算法还是同样的取模，只不过现在分桶分到的很可能是不存在的桶，那么就往下找找到第一个真实存在的桶放进去。这样 2 和 3 都被分到了编号为 3 的桶， 4 和 5 被分到了编号为 6 的桶。

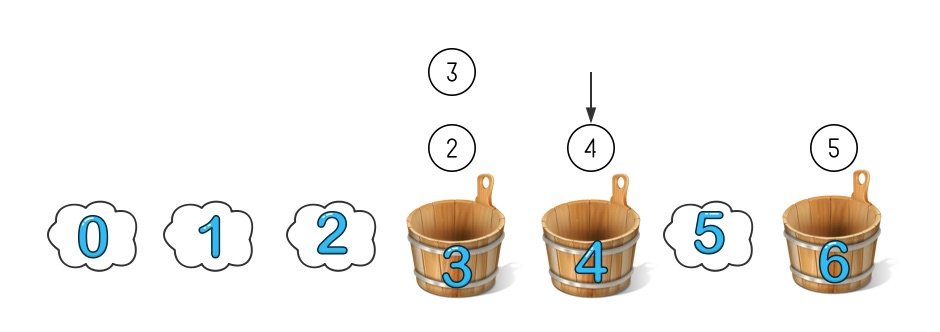
这时候再添加一个新的桶，编号是 4，取模方法不变还是模 7。因为 3 号桶里都是取模小于等于 3 的，4 号桶只需要从 6 号桶里拿走属于它的数字就可以了，这种情况下只需要调整一个桶的数字就可分成了重新分布。

升级: 这里还有个小问题要是编号为 6 的机桶下线了，它没有后一个桶了，数据该咋办？为了解决这个问题，实现上通常把哈希空间做成环状，

**时间复杂度: **

• 普通的哈希查询一次哈希计算就可以找到对应的桶了，算法时间复杂度是 O(1)，
• 一致性哈希需要将排好序的桶组成一个链表，然后一路找下去，k 个桶查询时间复杂度是 O(k)。可以用跳转表进行一个快速的跳转实现 O(logk) 的时间复杂度。

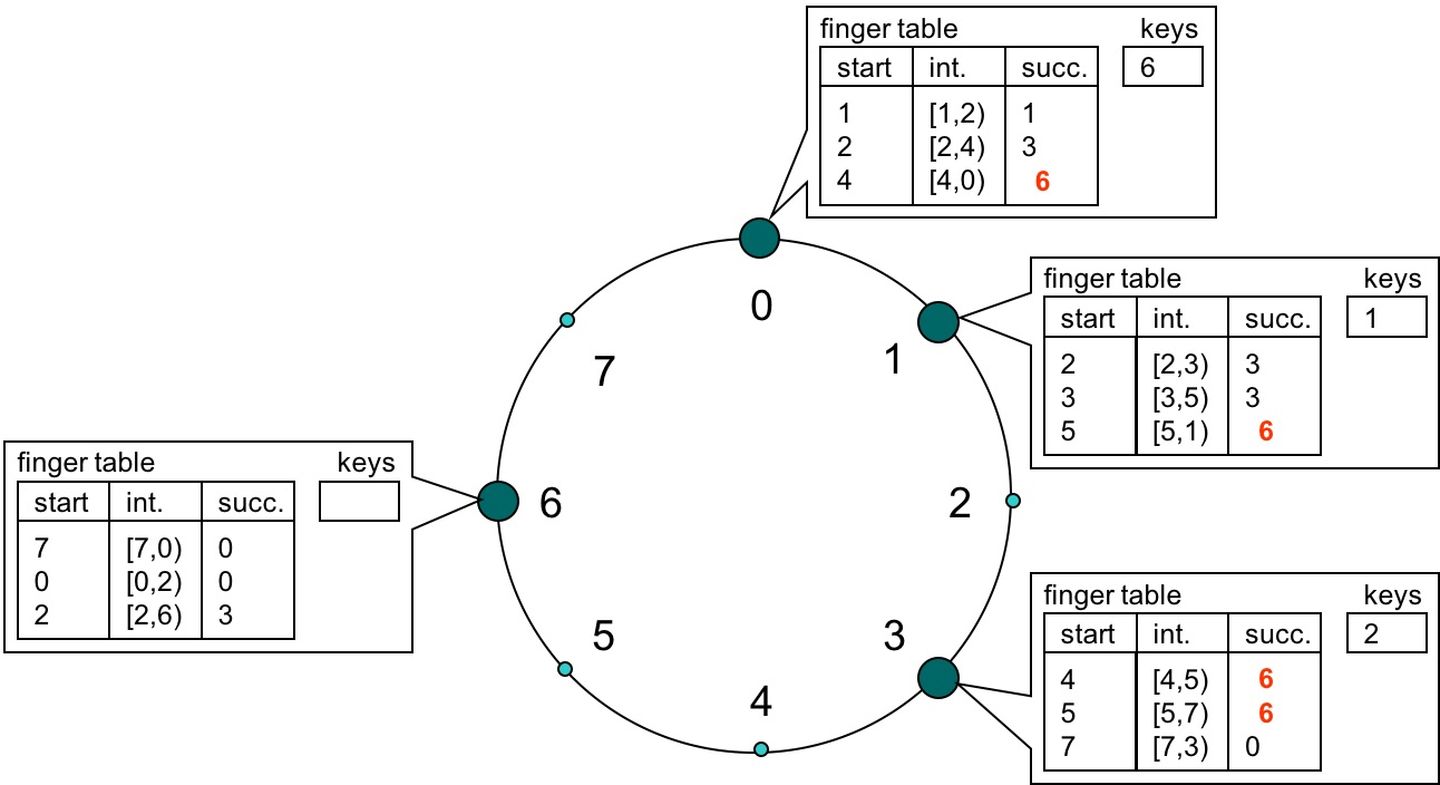
在这个跳转表中，每个桶记录距离自己 1，2，4 距离的数字所存的桶，这样不管查询落在哪个节点上，对整个哈希环上任意的查询一次都可以至少跳过一半的查询空间，这样递归下去很快就可以定位到数据是存在哪个桶上。

3、bit单位换算

• 1B=1字节=8bit（比特）。
• 1KB=1024B（KB：千节字，也写作“K”，可读作“K”）。
• 1MB（1M）=1024KB（MB：兆字节，也可写作“M”，读作“兆”）。
• 1GB（1G）=1024MB=1024兆(GB：吉字节，也可写作“G”，读作“G”或“吉”)。
• 1TB=1024GB（TB：万亿字节，读作“TB”或“千吉”）。

4、常见排序算法的空间时间复杂度

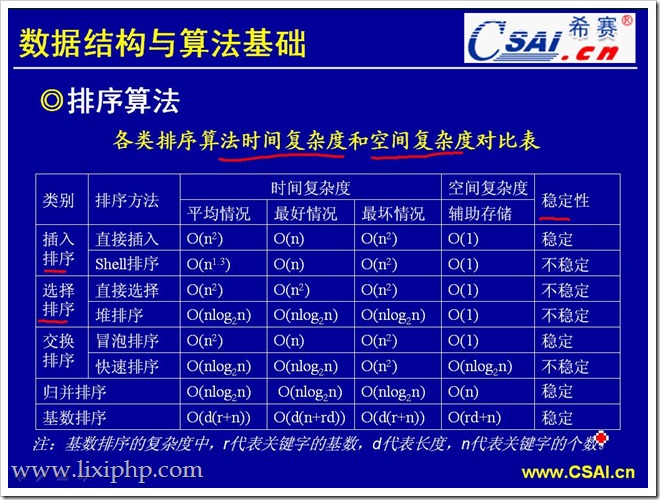
• 希尔排序又叫“缩小增量排序”，先取一个小于n的整数d1作为第一个增量，把文件的全部记录分成d1个组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序，然后取第二个增量d2。其是插入排序改良的算法，希尔排序步长从大到小调整，第一次循环后面元素逐个和前面元素按间隔步长进行比较并交换，直至步长为1，步长选择是关键。

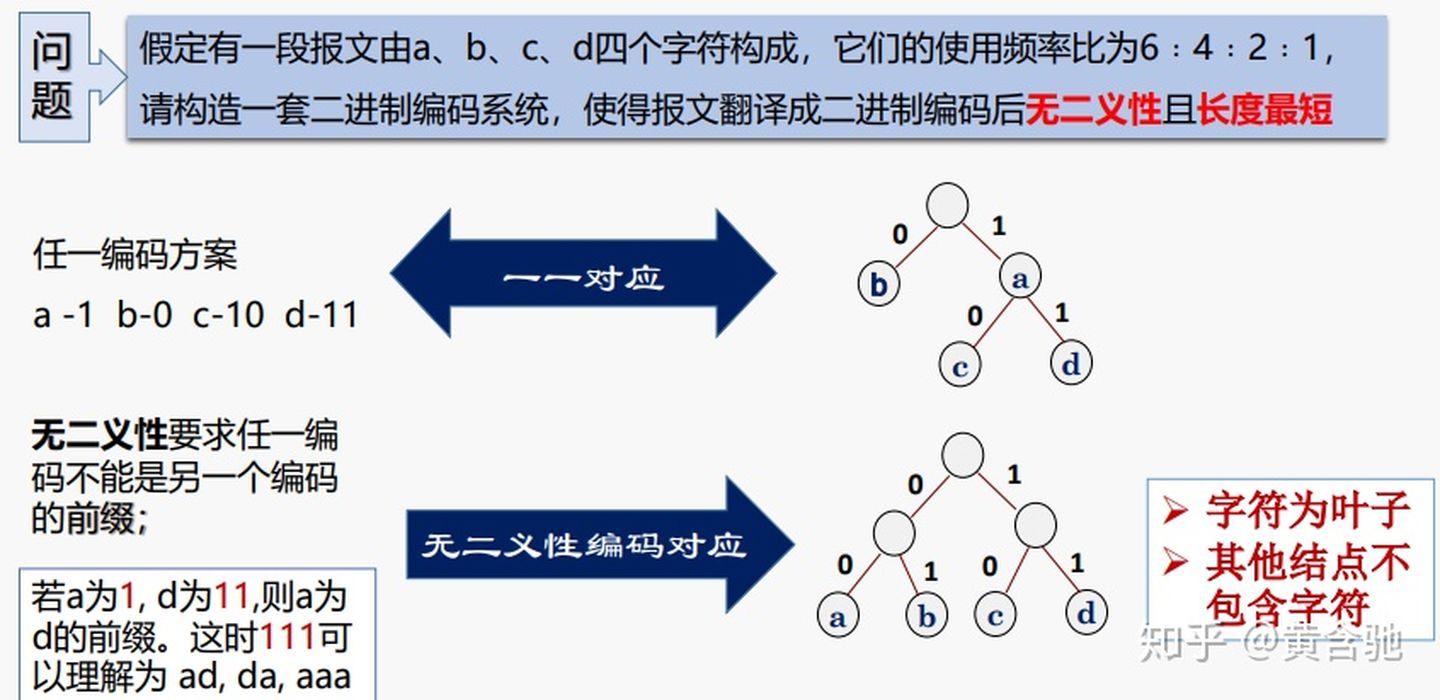
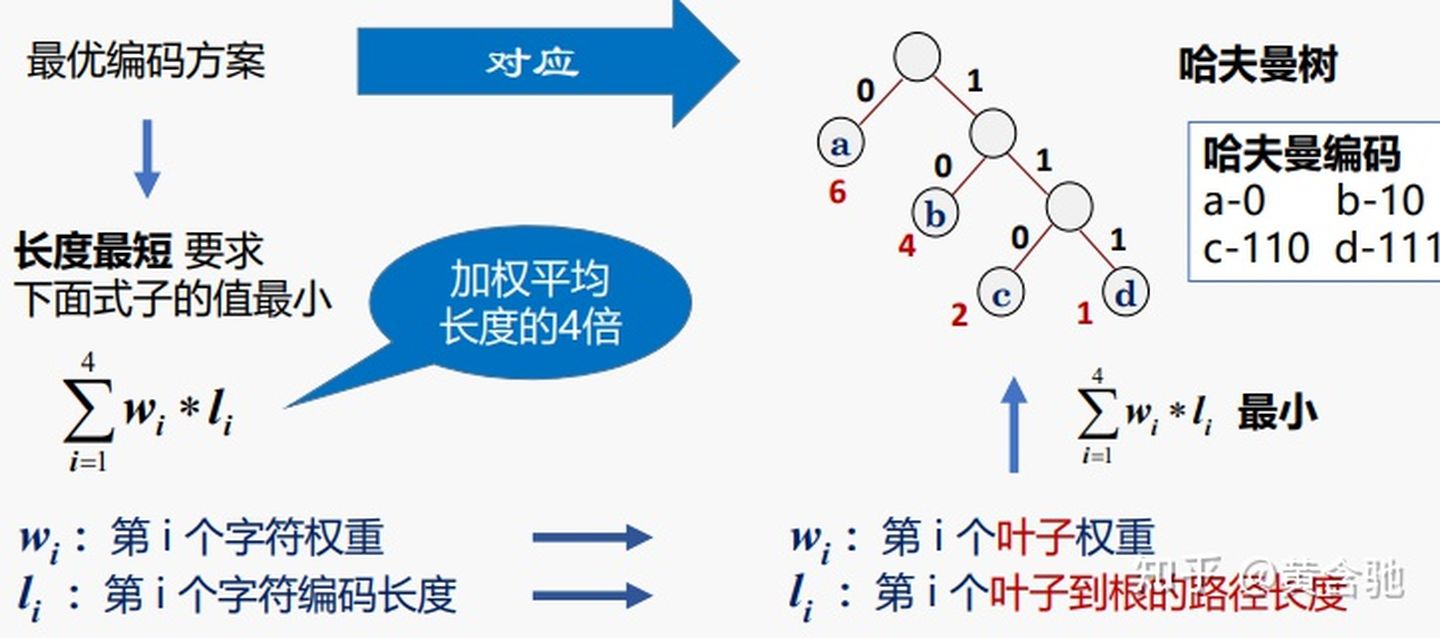
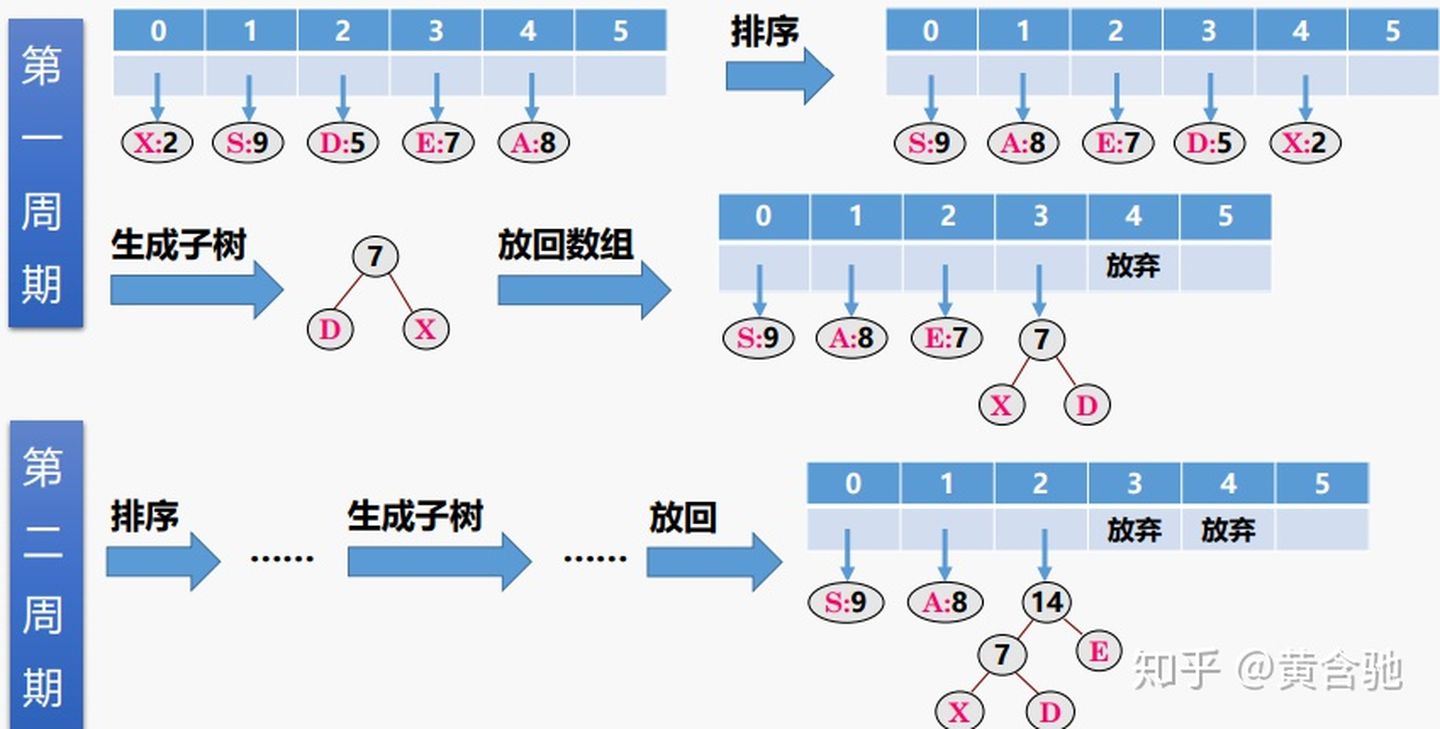
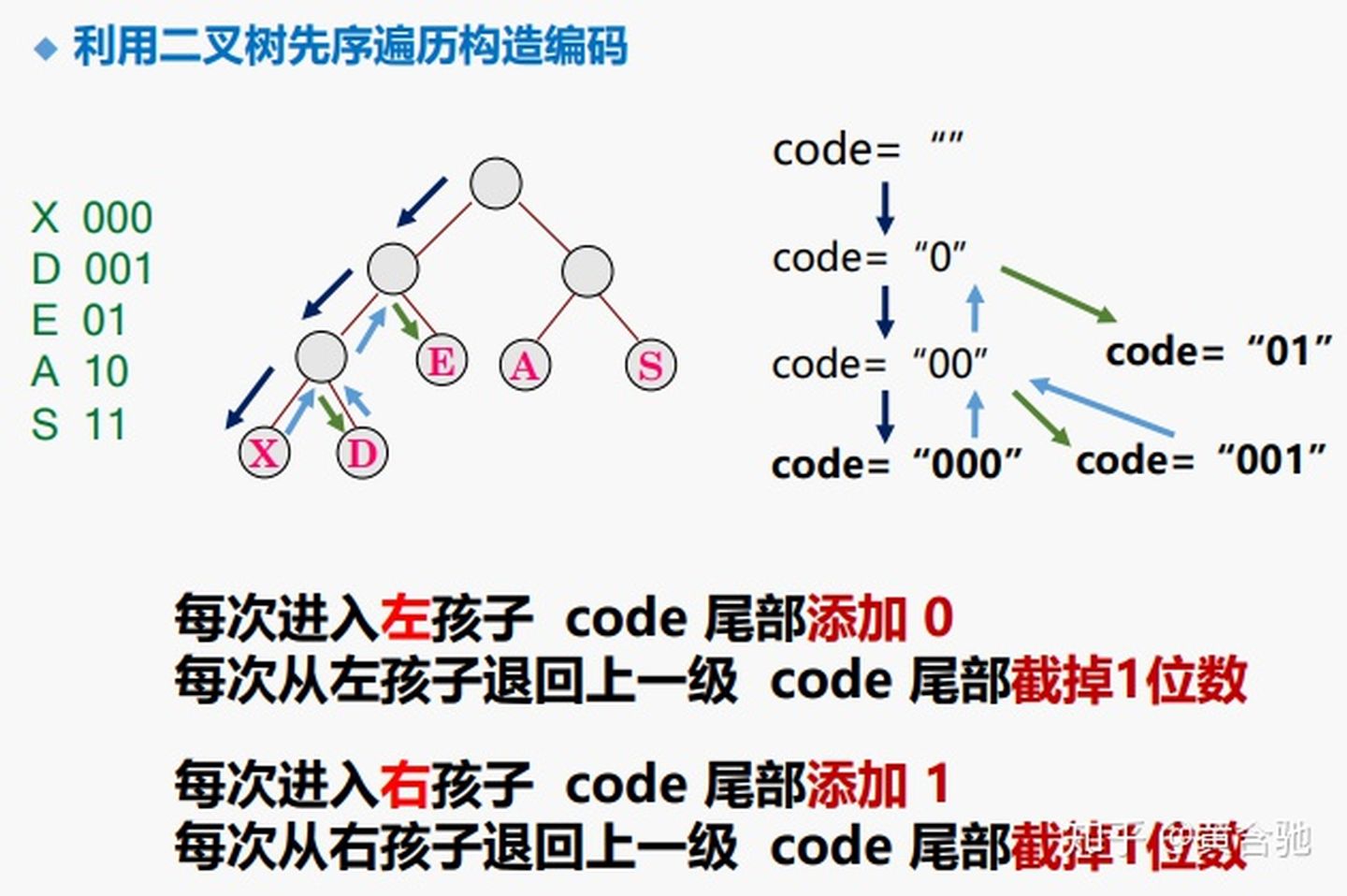
5、哈夫曼编码

数据压缩技术，编码思想：根据字符出现的概率大小进行编码，出现概率高的字符使用较短的编码，出现概率低的字符使用较长的编码。

6、树

平衡二叉树(AVL):

任何一个节点的左右子树的高度相差不超过1，又被称为AVL树

查找效率/高度为O（logn）。插入和删除节点可能需要做一次旋转动作

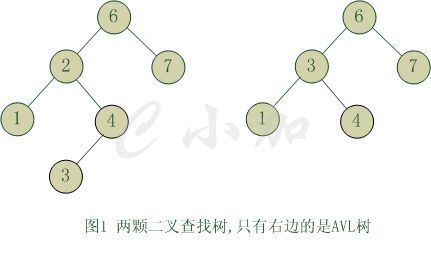
旋转: 增加、删除破坏其平衡性要进行旋转

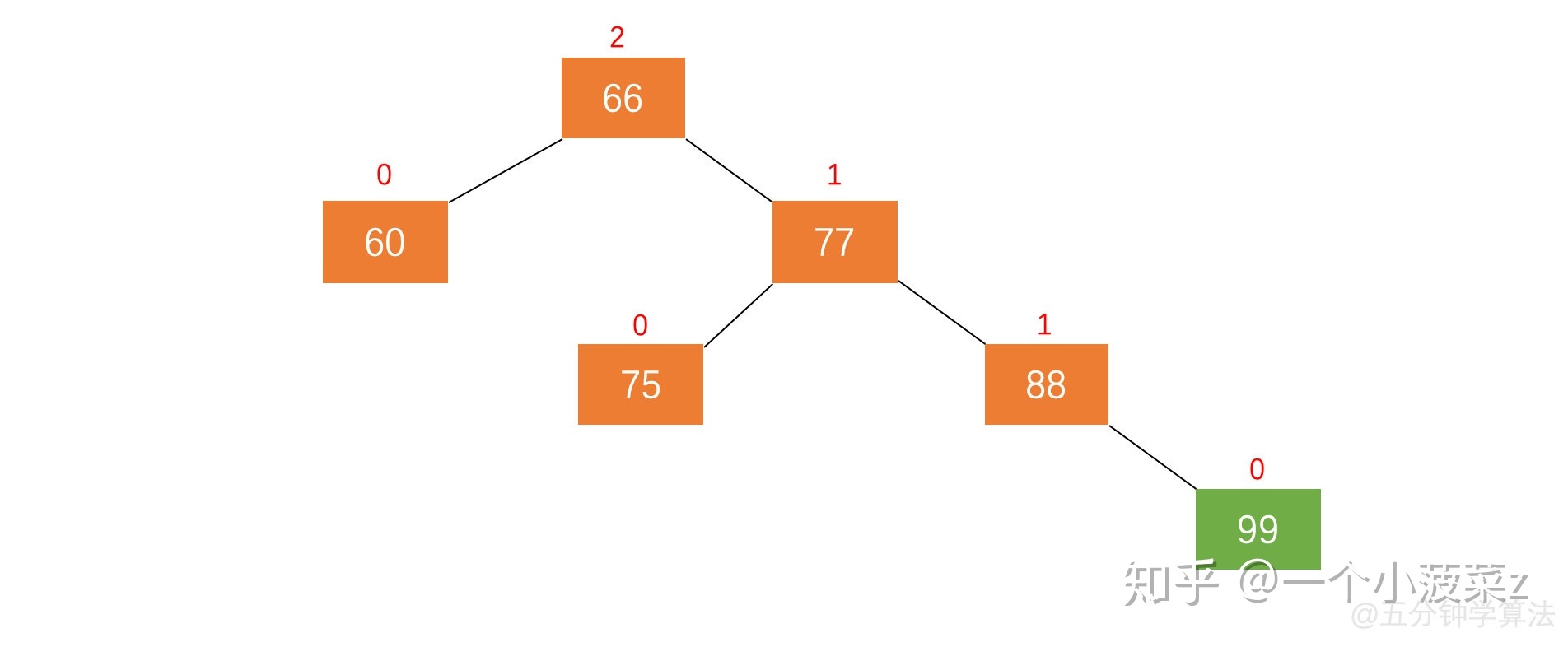
左旋:节点 66 的左子树高度为 1，右子树高度为 3，此时平衡因子为 -2。为保证树的平衡，此时需要对节点 66 做出旋转，因为右子树高度高于左子树，对节点进行左旋操作，流程如下：

• 节点的右孩子替代此节点位置
• 右孩子的左子树变为该节点的右子树
• 节点本身变为右孩子的左子树

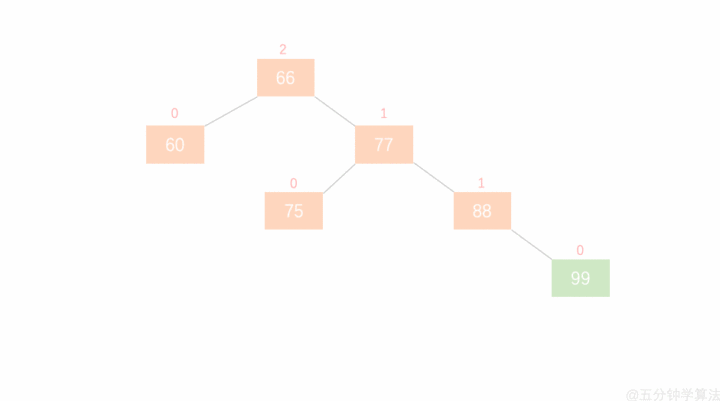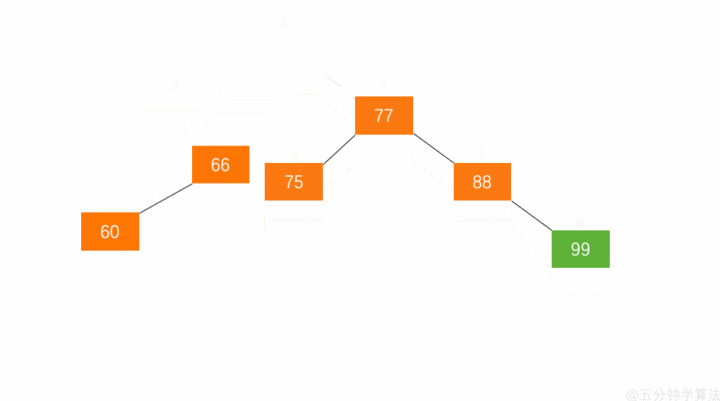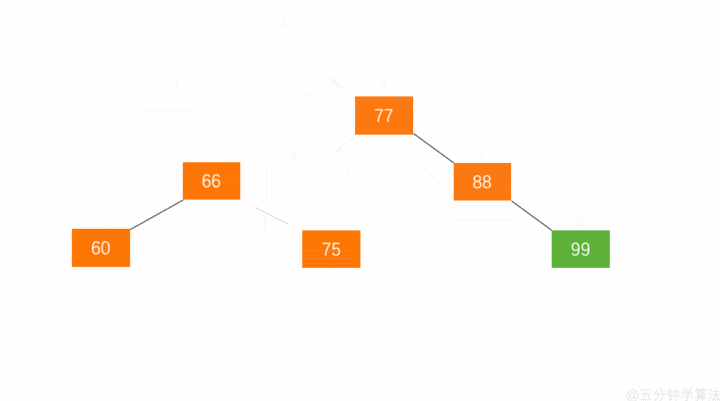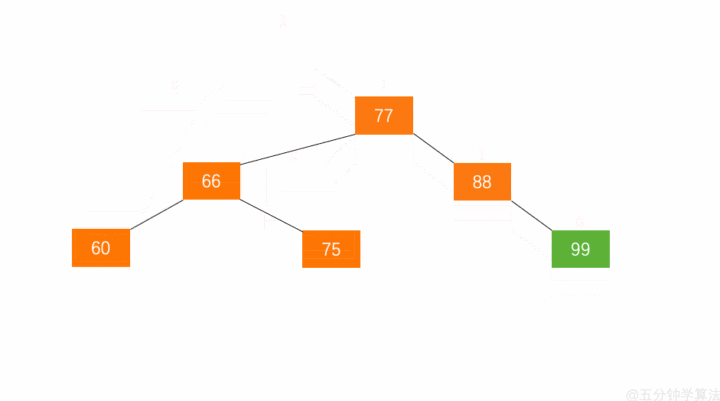
右旋:

• 节点的左孩子代表此节点
• 节点的左孩子的右子树变为节点的左子树
• 将此节点作为左孩子节点的右子树

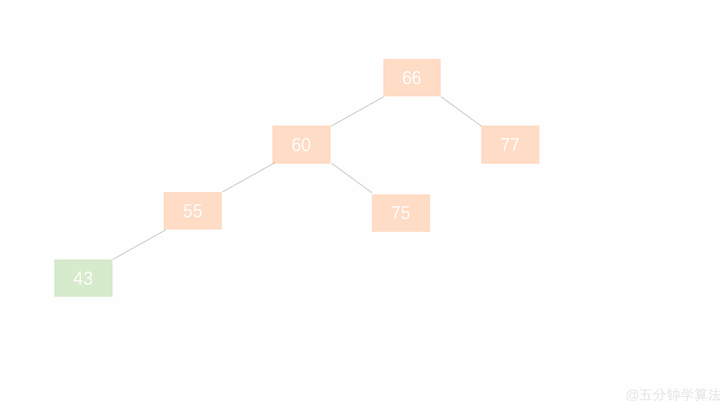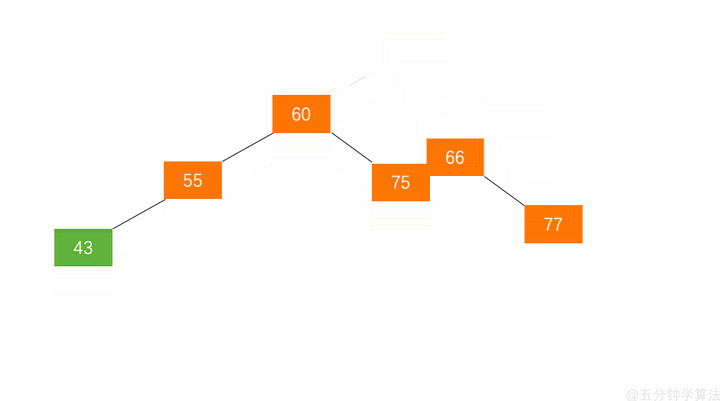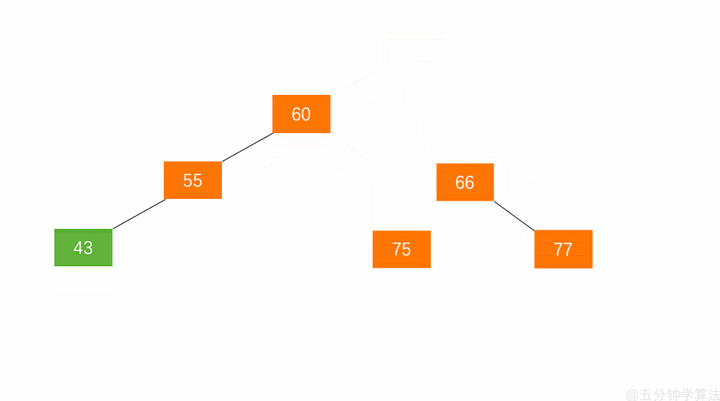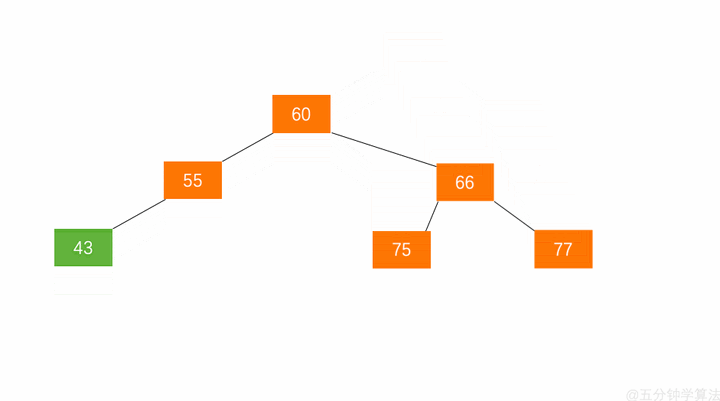
红黑树:

它的最坏情况运行时间也是非常良好的，并且在实践中是高效的： 它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目

查找的时间复杂度为2log(n+1)

插入和删除的时间为O(logn)

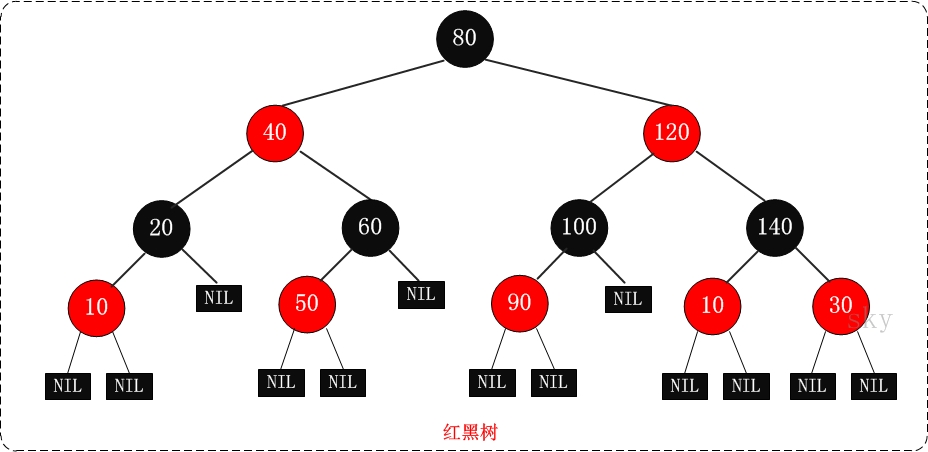
• 每个节点或者是黑色，或者是红色。
• 根节点是黑色。
• 每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
• 如果一个节点是红色的，则它的子节点必须是黑色的。
• 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
  • 确保没有一条路径会比其他路径长出俩倍。因而，红黑树是相对是接近平衡的二叉树

定理:

• 一棵含有n个节点的红黑树的高度至多为2log(n+1).

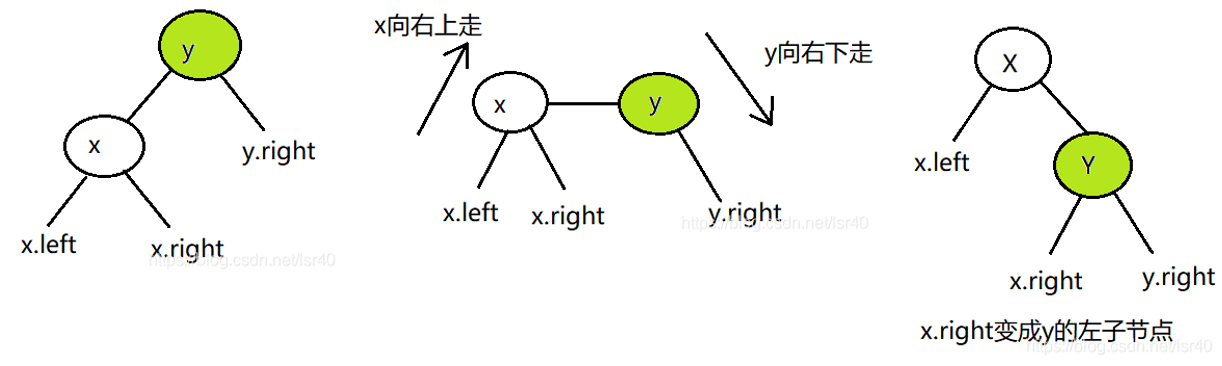
左旋:

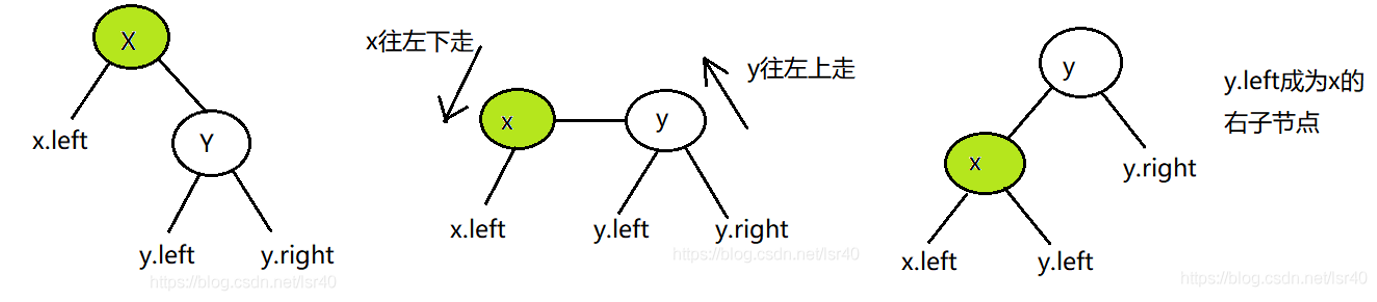
右旋:

应用

• set/map：红黑树
• linux调度: 红黑树往往出现由于树的深度过大而造成磁盘IO读写过于频繁，进而导致效率低下的情况在数据较小，可以完全放到内存中时，红黑树的时间复杂度比B树低
• Trie树(字典树): 用在统计和排序大量字符串，如自动机。

AVL树和RB树之间的区别:

• AVL树的结构相较于RB树来说更加平衡，所以在插入或者删除一个node的时候更容易引起树的不平衡，导致更高频率的rebalance操作,RB树只需做有限的旋转操作和变色操作即可，所以在插入和删除节点的时候使用RB树效率更高
• 查找效率方面，RB树是黑色节点平衡的，所以平衡度没有AVL高，查找的次数上可能会比AVL更多一些
• 红黑树的查询性能略逊色于平衡二叉树，但是在相同的条件下也最多多一次比较，但是红黑树在插入和删除上是完胜平衡二叉树的，平衡二叉树每加入或删除一个节点都需要耗费大量的平衡计算开销；而红黑树在节点旋转和颜色变换上付出的开销是要远小于AVL的。

为什么说红黑树是“近似平衡”的

• 对于AVL树，任何一个节点的两个子树高度差不会超过1；
• 对于红黑树，则是不会相差两倍以上，从而在这样的树中进行搜索的话即便在最坏情况下也会很高效，这就足够了。

B树：

• B树是所有节点的平衡因子均等于0的多路查找树
• AVL树是平衡因子不大于 1 的二路查找树
• 从磁盘查找的效率来讲，查找、插入和删除操作的时间复杂度都要小于二叉树
• B+树是B树的变种树，有n棵子树的节点中含有n个关键字，每个关键字不保存数据，只用来索引，数据都保存在叶子节点。是为文件系统而生的。且叶子结点用链表串连
• B树应用文件系统中，B+树用于索引

B+树

• 节点存的不一样； b+tree 只有叶子节点存数据，中间节点存key值
• 叶子节点顺序查询

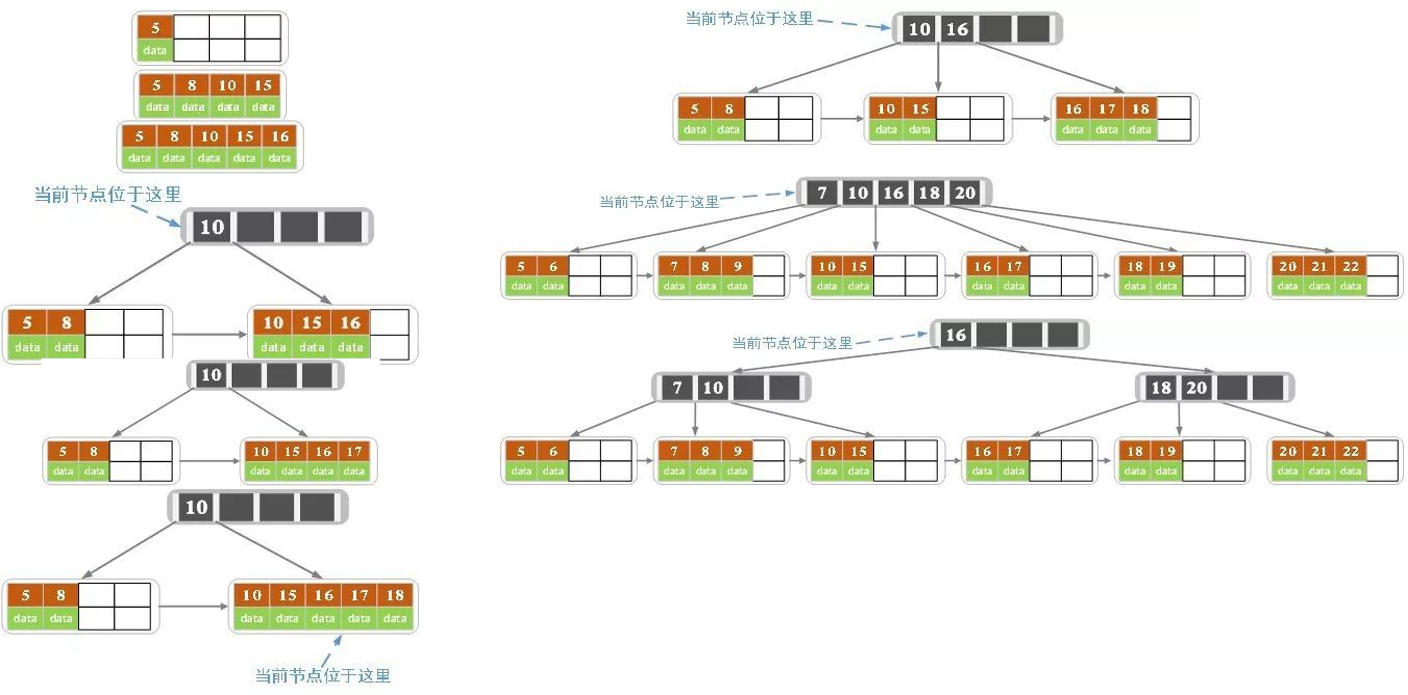
B+树的插入过程

二叉堆

• 二叉堆本质上是一种完全二叉树

• 最大堆：任何一个父节点的值，都大于等于它左右孩子节点的值

• 最小堆：任何一个父节点的值，都小于等于它左右孩子节点的值

• 堆（heap），堆通常可以看作为一棵树，但这棵树得满足以下条件：

  • 堆中任意节点的值总是不大于（不小于）其子节点的值；
  • 堆总是一颗完全树
  • 更简便的存储方式（数组）：
    • 索引为 i 的左孩子的索引为（2i + 1）
    • 索引为 i 的右孩子的索引为 （2i + 2）
    • 索引为 i 的父节点的索引为 （i - 1）/ 2（计算机里取整）

7、KMP算法

KMP算法是用来进行字符串匹配查找的，比如在字符串1中查找是否包含字符串2。核心是先求出Next数组。什么是next数组？我的理解是：

next数组表示的是待查找的字符串的最大公共前后缀中的公共前缀的最后一个字符的下标，知道这个下标，就可以知道当匹配目标字符串出错时，目标字符串的指针怎么回退，而查找段落的指针不用回退，这样遍历一遍查找段落，就可以知道是否存在目标字符串，时间复杂度为O（n）

例如，求目标字符串ababc的next数组，下标从0开始。

• 比如next[2]，2位置为a，则next[2]表示0位置的a（因为aba的最长公共前缀为a），next[2] =0。

• 比如next[3]，3位置为b，则next[3]表示1位置的b（因为abab的最长公共前缀为ab), next[3] = 1。

• 比如next[4]，由于4位置为c，而ababc没有公共前后缀，则next[4]=-1。

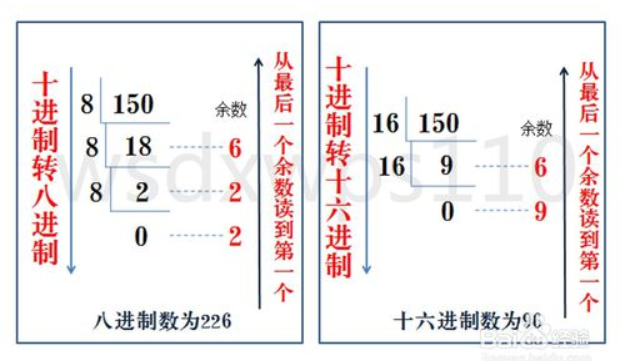
8、进制转换

除留余数法

9、char、int、long、float、double所占字节数

	32位	64位
char	1	1
int	4	大多数为4、少数为8
long	4	8
float	4	4
Double	8	8
指针	4	8