Paxos算法
1、CAP理论
分布式架构中有一个基础的CAP理论,也就是我们的系统最多只能满足数据一致性(Consistency)、可用性(Availability)和网络分区容忍(Partition Tolerance)三个特性中的两个
一致性: 所有节点在同一时间的数据完全一致
- 一致性是在并发读写时才会出现的问题,因此在理解一致性的问题时,一定要注意结合考虑并发读写的场景。
可用性: 用户访问数据时,系统是否能在正常响应时间返回结果
分区容错性:分布式系统在遇到某节点或网络分区故障的时候,仍然能够对外提供满足一致性和可用性的服务,即一份数据要放到网络中的所有节点中去,一个数据项复制到多个节点上,P一定满足
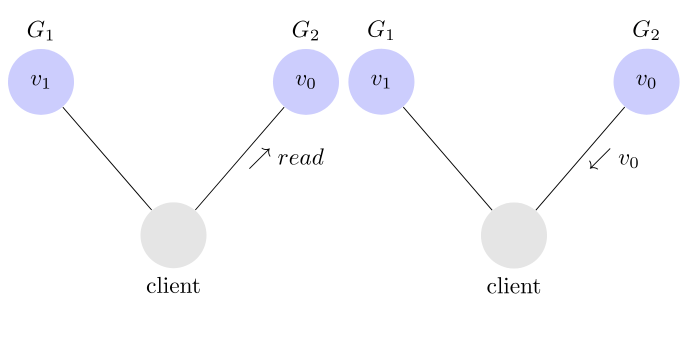
如果保证 G2 的一致性,那么 G1 必须在写操作时,锁定 G2 的读操作和写操作。只有数据同步后,才能重新开放读写。锁定期间,G2 不能读写,没有可用性不。
如果保证 G2 的可用性,那么势必不能锁定 G2,所以一致性不成立。
综上所述,G2 无法同时做到一致性和可用性。系统设计时只能选择一个目标。如果追求一致性,那么无法保证所有节点的可用性;如果追求所有节点的可用性,那就没法做到一致性。
常见分布式算法
- Zookeeper: CP
- Raft: 满足CP的情况下,尽可能提高A
2、BASE理论
BASE理论是对CAP中的一致性及可用性进行一个权衡的结果,其核心思想是:我们无法做到强一致性,那么我们可以通过牺牲强一致性获得可用性, 一般应用于服务化系统的应用层或者大数据处理系统中,采用适当的方式达到最终一致性
BA: Basically Available(基本可用)
基本可用:是对A(可用性)的一个妥协,比如秒杀场景下,或者雪崩的业务场景下,可以降级处理,使核心功能可用,而不是所有的功能可用。或者延迟完成,比如通过削峰限流,来延迟响应S: Soft state(软状态)
指允许部分节点数据存在一定的延时,这个延时不影响可用性
例如一次写操作只更新了一个结点就返回成功。那么其他节点和这个节点的数据时不一致的。此时的数据状态就是软状态。该状态不能一直存在,必须要有个期限,系统保证在没有后续更新的前提下,在这个期限后,系统最终返回上一次更新操作的值,从而达到数据的最终一致性,这个容忍期限(不一致窗口的时间)取决于通信延迟,系统负载,数据复制方案设计,复制副本个数等,DNS是一个典型的最终一致性系统
E: Eventually consistent(最终一致性)
指最终数据要实现一致性,例如:软状态的数据最终我们要通过一些手段将数据同步到其他数据节点上。例如使用mq。
3、Paxos不考虑拜占庭将军问题(Leslie Lamport)
一组拜占庭将军分别各率领一支军队共同围困一座城市。为了简化问题,将各支军队的行动策略限定为进攻或撤离两种。因为部分军队进攻部分军队撤离可能会造成灾难性后果,因此各位将军必须通过投票来达成一致策略,即所有军队一起进攻或所有军队一起撤离。因为各位将军分处城市不同方向,他们只能通过信使互相联系。在投票过程中每位将军都将自己投票给进攻还是撤退的信息通过信使分别通知其他所有将军,这样一来每位将军根据自己的投票和其他所有将军送来的信息就可以知道共同的投票结果而决定行动策略。
系统的问题在于,可能将军中出现叛徒,他们不仅可能向较为糟糕的策略投票,还可能选择性地发送投票信息。假设有9位将军投票,其中1名叛徒。8名忠诚的将军中出现了4人投进攻,4人投撤离的情况。这时候叛徒可能故意给4名投进攻的将领送信表示投票进攻,而给4名投撤离的将领送信表示投撤离。这样一来在4名投进攻的将领看来,投票结果是5人投进攻,从而发起进攻;而在4名投撤离的将军看来则是5人投撤离。这样各支军队的一致协同就遭到了破坏。
一个将军怎么根据自己所知的信息进行进攻或者撤退
4、Paxos角色:
- Proposer:提案者
- Acceptor: 表决者
- Learner: 同步者
5、Paxos数据一致性体现在以下几点:
- 每个提案者在提出提案时都会首先获取到一个具有全局唯一性的、递增的提案编号 N, 即在整个集群中是唯一的编号 N,然后将该编号赋予其要提出的提案。
- 每个表决者在 accept 某提案后,会将该提案的编号 N 记录在本地,这样每个表决者中保存的已经被 accept 的提案中会存在一个编号最大的提案,其编号假设为 maxN。每个表决者仅会 accept 编号大于自己本地 maxN 的提案。
- 在众多提案中最终只能有一个提案被选定。
- 一旦一个提案被选定,则其它服务器会主动同步(Learn)该提案到本地。
- 没有提案被提出则不会有提案被选定
6、过程:
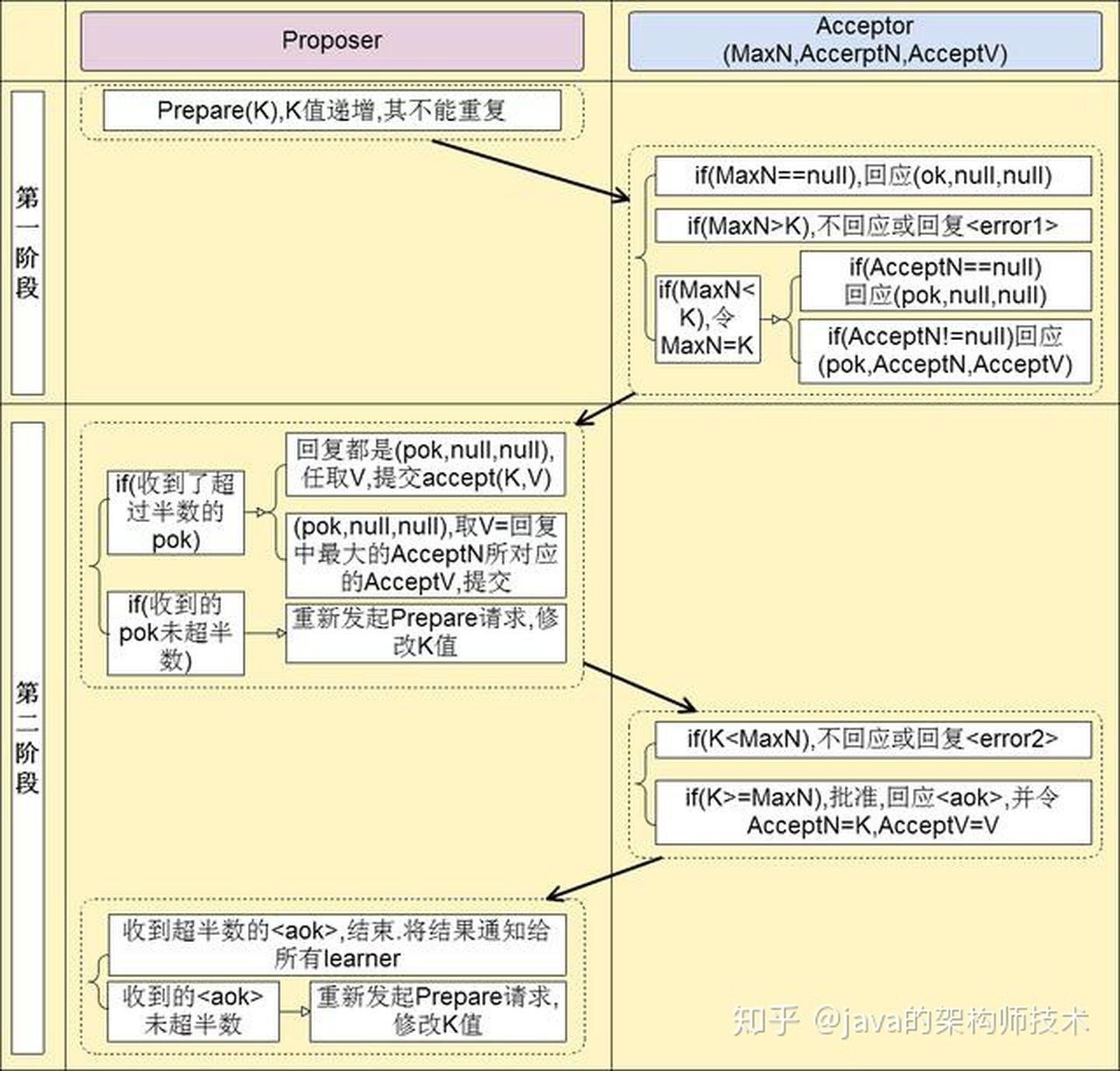
第一阶段(预提案):
提案者先选择一个提案编号N,并且将该编号的预提交请求Prepare(N)发送给表决者。
表决者收到预提案请求Prepare(N),比较存储的最大提案编号PN与N的关系:
如果PN < N,则先令PN = N,并且同意提议者请求,发送表决者的最大提案编号PN(等于N)和最后一个批准的数据Value(可能为空)。
否则,拒绝请求,同样发送发送当前长老们的最大提案编号PN(等于N)和最后一个批准的数据Value(可能为空)。这个部分的意思就好比是逐个表决,及时更新赞同最多的方案。
第二阶段(提案):
当预提案Prepare(N)被大多数表决者同意时(PN=N),则做出以下提案:
如果所有接收到的PrepareResponse(PN, Value)中Value全部为空(表决者还未批准任何提案),则自己制定一个该值的取值Vn,并向表决者集合发送提案:Proposal(N, Vn)
如果接收到的PrepareResponse(PN, Value)集合中存在不为空的Value,则选取Value不为空的PrepareResponse(PN, ValueNotNull)集合中PN最大的值(PNmax, ValueNotNull),并将其作为提案发送给表决者:Proposal(PNmax, ValueNotNull)
如果一个表决者接收到一个提案编号为N的提案Proposal(N, Vn)则:
- 如果PN为空或者PN < N,则先令PN = N,Value = Vn,并且通过该条提案,返回:ProposalResponse(PN, Value)
- 如果PN == N并且Value为空(尚未批准提案号为PN的任何提案),则先令Value = Vn,并且通过该条提案,返回:ProposalResponse(PN, Value)
- 如果PN > N则拒绝该提案,回:ProposalResponse(PN, Value)
7、活锁和选主
当某一提案者提交的提案被拒绝时,可能是因为表决者 承诺返回了更大编号的proposal,因此proposer提高编号继续提交。 如果2个提案者都发现自己的编号过低转而提出更高编号的提案者,会导致死循环,这种情况也称为活锁
为了保证流程的执行,我们必须选出一个主提案者,作为提案的唯一人选。如果主提案者能和大数派的集合进行通信,并且使用了一个比所有已经批准的提案号都大的编号,那么它就能成功产生被接受的提案